 Suites numériques, modèles discrets
Suites numériques, modèles discrets
A SAVOIR: le cours sur les suites
Exercice 7
Un radiateur a une température initiale de 60 °C dans une pièce dont la température, supposée constante, est égale à 20 °C.
Le chauffage ne fonctionne pas et le radiateur va refroidir. On conçoit que sa température va diminuer et tendre lentement vers 20 °C.
La loi de refroidissement de Newton, énoncée par Isaac Newton (1642-1727), affirme que le taux d'évolution de la température d’un corps est proportionnel à la différence entre la température de ce corps
et celle du milieu environnant.
Pour tout entier naturel $n$, on note $t_n$ la température ( en °C) du radiateur à l’instant $n$ (en minutes) .
On a ainsi $t_0=60$.
On modélise la loi de Newton entre deux minutes consécutives quelconques $n$ et $n+1$ par l'égalité:
$t_{n+1}-t_n=-0,01(t_n-20)$
Le coefficient de proportionnalité $-0,01$ est lié à la géométrie et à la matière du radiateur.
- Déterminer $t_1$, $t_2$ et $t_3$.
La phrase "Le radiateur refroidit de plus en plus vite" est-elle vraie? - Montrer que la suite $(t_n)$ est arithmético-géométrique de paramètres $a=0,99$ et $b=0,2$
- Exprimer $t_n$ en fonction de $n$ pour tout naturel $n$
- Montrer que la suite $(t_n)$ est strictement décroissante.
- Déterminer $\lim↙{n→+∞}(u_n)$ et conclure.
- A partir d'un certain temps, la température du radiateur va passer en dessous de 21 °C. Donner une explication mathématique à ce fait.
- Le programme suivant, écrit en Python, est sensé proposer une fonction duree(temp) qui renvoie un entier $n$ à partir duquel les termes de la suite sont strictement inférieurs à $temp$.
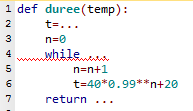
Corriger les lignes 2, 4 et 7 du programme pour qu'il fonctionne correctement.
Programmer la fonction et donner la valeur qu'elle renvoie si temp=21.
Corrigé
Clique ICI pour revoir l'essentiel sur les suites arithmético-géométriques.
- On a: $t_1-t_0=-0,01(t_0-20)$, et donc: $t_1=t_0-0,01(t_0-20)$
Soit: $t_1=60-0,01×(60-20)=59,6$
On a: $t_2-t_1=-0,01(t_1-20)$, et donc: $t_2=t_1-0,01(t_1-20)$
Soit: $t_2=59,6-0,01×(59,6-20)=59,204$
On a: $t_3-t_2=-0,01(t_2-20)$, et donc: $t_3=t_2-0,01(t_2-20)$
Soit: $t_3=59,204-0,01×(59,204-20)=58,81196$
On a donc: : $t_0-t_1=0,4$, $t_1-t_2=0,396$ et $t_2-t_3=0,39204$.
Ces variations sont de plus en plus faibles. Donc la phrase "Le radiateur refroidit de plus en plus vite" est fausse. La loi de refroidissement de Newton exprime au contraire le fait que "le radiateur refroidit de moins en moins vite". - $t_{n+1}-t_n=-0,01(t_n-20)$ $⇔$ $t_{n+1}=t_n-0,01t_n+0,01×20$ $⇔$ $t_{n+1}=0,99t_n+0,02$
Donc, pour tout naturel $n$, on a: $t_{n+1}=0,99t_n+0,2$
Donc la suite $(t_n)$ est arithmético-géométrique de paramètres $a=0,99$ et $b=0,2$ - Recherchons une formule explicite pour $(t_n)$ en 3 étapes.
Etape 1
On a: $l=al+b$ $⇔$ $l=0,99l+0,2$ $⇔$ $0,01l=0,2$ $⇔$ $l={0,2}/{0,01}=20$
Etape 2
On considère alors la suite $v_n$ définie par $v_n=t_n-20$, pour tout naturel $n$.
Montrons que la suite $(v_n)$ est géométrique de raison $a=0,99$.
Soit $n$ un entier naturel; $v_{n+1}=t_{n+1}-20=0,99×t_n+0,2-20=0,99×t_n-19,8$.
Or: $0,99×v_n=0,99×(t_n-20)=0,99×t_n-0,99×20=0,99×t_n-19,8$.
Donc: $v_{n+1}=0,99×v_n$, et ceci est vrai pour tout entier naturel $n$.
Donc $(v_n)$ est bien géométrique de raison $0,99$.
Etape 3
Notons que $v_0=t_0-20=60-20=40$.
Comme $(v_n)$ est géométrique de raison $0,99$ et de premier terme $40$, on obtient: $v_n=40×0,99^n$.
Par ailleurs, comme $v_n=t_n-20$, on obtient: $v_n+20=t_n$.
Ce qui donne finalement: $40×0,99^n+20=t_n$. - Comme 0<0,99<1, la suite $(0,99^n)$ est strictement décroissante.
Comme $40>0$, la suite $(40×0,99^n)$ est également strictement décroissante.
Et par là, la suite $(t_n)$ est aussi strictement décroissante. - Comme 0<0,99<1, on a: $\lim↙{n→+∞}(0,99^n)=0$.
Donc: $\lim↙{n→+∞}(t_n)=40×0+20$ Soit: $\lim↙{n→+∞}(t_n)=20$.
La température du radiateur tend vers 20 °C, ce qui est conforme à l'intuition. - Comme $\lim↙{n→+∞}(t_n)=20$, tous les termes $t_n$ deviennent aussi proches de $20$ que l'on veut pourvu que $n$ soit suffisamment grand.
Donc, à partir d'un certain temps, la température du radiateur va passer en dessous de 21 °C.
La raison n'est pas la stricte décroissance de la suite $(t_n)$. Elle pourrait en effet être strictement décroissante sans jamais passer en dessous de 21! - Voici un programme convenable.

La ligne 9 permet, à l'exécution du programme, d'afficher le résultat demandé dans la console. On peut s'en dispenser et écrire directement duree(21) derrière l'invite de commande de la console.
Si temp=21, alors la fonction renvoie 368.
La température du radiateur va passer en dessous de 21 °C au bout de 368 minutes (6 heures et 8 minutes).