 Arithmétique
Arithmétique
I Divisibilité
a. Généralités
Définitions
Soient $a$ et $b$ deux entiers relatifs.
$a$ est un diviseur de $b$ s'il existe un entier relatif $k$ tel que $b=ka$.
On dit aussi que $a$ divise $b$.
On dit aussi que $b$ est un multiple de $a$.
O ne divise aucun nombre relatif à part lui-même.
Tout nombre relatif divise 0.
Propriété
Soient $a$ et $b$ deux entiers relatifs.
Si $a$ divise $b$, alors les multiples de $b$ sont des multiples de $a$, et les diviseurs de $a$ sont des diviseurs de $b$.
 Exemple
Exemple
6 divise 30. Or 60 est un multiple de 30. Donc 6 divise 60.
6 divise 30. Or 3 est un diviseur de 6. Donc 3 divise 30.
Propriété
Soient $a$ et $b$ deux entiers relatifs.
Si $a$ divise $b$, alors $-a$ divise $b$, $a$ divise $-b$, $-a$ divise $-b$.
Propriété
Si $b$ est un entier relatif non nul, alors il possède un nombre fini de diviseurs, tous compris entre $-b$ et $b$.
Propriété
Soient $a$, $b$ et $c$ trois entiers relatifs.
Si $a$ divise $b$ et $b$ divise $c$, alors $a$ divise $c$.
Divisibilité et combinaison linéaire
Soient $a$, $b$ et $c$ trois entiers relatifs.
Si $a$ divise $b$ et $c$, alors, pour tous entiers relatifs $u$ et $v$, $a$ divise $bu+cv$
 Exemple
Exemple
Montrons que, si $a$ divise 2 entiers consécutifs, alors $a=1$ ou $a=-1$.
Supposons que $a$ divise $n$ et $n+1$. Alors il divise $(-1)×n+1×(n+1)$, c'est à dire $1$.
Par conséquent: $a=1$ ou $a=-1$.
Méthode
Une combinaison linéaire bien choisie permet d'éliminer une inconnue gênante ( l'inconnue $n$ dans l'exemple ci-dessus ).
b. Division euclidienne
Division euclidienne
Soient $a$ un entier relatif et $b$ un entier naturel non nul.
Il existe un unique couple d'entiers relatifs $(q;r)$ tel que: $a=qb+r$ et $0≤r < b$
$q$ s'appelle le quotient et $r$ s'appelle le reste de la division euclidienne de $a$ par $b$.
 Exemple
Exemple
Posons $a=33$ et $b=8$. Effectuons la division euclidienne de $a$ par $b$.
On a: $a=33=4×8+1=4×b+1$ et $0≤1 < b$
Le quotient de la division euclidienne de $a$ par $b$ est $q=4$, et le reste est $r=1$.
Propriété
Soient $a$ un entier relatif et $b$ un entier naturel non nul.
$b$ divise $a$ si et seulement si le reste de la division euclidienne de $a$ par $b$ est nul.
Propriété
Les restes possibles de la division euclidienne d'un entier relatif $a$ par un entier naturel non nul $b$ sont:
$0$ , $1$ , $2$ , ... , $b-1$.
Et par là, tout entier relatif $a$ peut s'écrire:
soit: $bk$ , soit: $bk+1$ , soit: $bk+2$ , ... , soit: $bk+b-1$ (où $k$ est un entier relatif)
 Exemple
Exemple
Soit $n$ un entier naturel. On pose: $x=n(n^2+5)$.
Montrer que $x$ est divisible par 3.
Corrigé
$n$ peut s'écrire soit $3k$, soit $3k+1$, soit $3k+2$ (où $k$ est un entier naturel).
-
Si $n=3k$, alors :
$x=3k(9k^2+5)=3k'$, avec $k'=k(9k^2+5)$ entier naturel.
On constate donc que $x$ est bien divisible par 3. -
Si $n=3k+1$, alors :
$x=(3k+1)(9k^2+6k+1+5)=(3k+1)(9k^2+6k+6)=3(3k+1)(3k^2+2k+2)=3k'$, avec $k'=(3k+1)(3k^2+2k+2)$ entier naturel.
On constate donc que $x$ est bien divisible par 3. -
Si $n=3k+2$, alors :
$x=(3k+2)(9k^2+12k+4+5)=(3k+2)(9k^2+12k+9)=3(3k+2)(3k^2+4k+3)=3k'$, avec $k'=(3k+2)(3k^2+4k+3)$ entier naturel.
On constate donc que $x$ est bien divisible par 3.
On a donc prouvé que, dans tous les cas, $x$ est divisible par 3.
La démonstration proposée ici est une démonstration par "disjonction de cas".
c. Congruences
Congruence dans $\ℤ$
Soient $a$ et $b$ deux entiers relatifs et $n$ un entier naturel non nul.
$a$ est congru à $b$ modulo $n$ si et seulement si $a$ et $b$ ont le même reste dans la division euclidienne par $n$.
Dans ce cas, on note: $a≡b$ $[n]$
Propriété
Soient $a$ et $b$ deux entiers relatifs et $n$ un entier naturel non nul.
$a≡b$ $[n]$ si et seulement si $a-b$ est un multiple de $n$.
$a≡b$ $[n]$ si et seulement si il existe un entier relatif $k$ tel que $a-b=kn$.
 Exemple
Exemple
Montrons que $14≡20$ $[3]$.
$14≡20$ $[3]$ car 14 et 20 ont le même reste (2) dans la division euclidienne par 3.
Autre méthode: la différence $14-20$ est un multiple de 3 (car $14-20=(-2)×3$). Donc $14≡20$ $[3]$
Propriété
Soient $a$ , $b$ et $c$ trois entiers relatifs et $n$ un entier naturel non nul.
$a≡0$ $[n]$ si et seulement si $a$ est divisible par $n$.
$a≡a$ $[n]$.
$r$ est le reste de la division euclidienne de $a$ par $n$ si et seulement si $a≡r$ $[n]$ et $0≤r < n$.
Si $a≡b$ $[n]$, et si $b≡c$ $[n]$, alors $a≡c$ $[n]$.
 Exemple
Exemple
3 et 5 sont des diviseurs de 15. Donc: $15≡0$ $[3]$ et: $15≡0$ $[5]$
on sait que: $265≡209$ $[7]$ , et: $209≡6$ $[7]$. On peut en déduire que: $265≡6$ $[7]$
Vérification pour les sceptiques: $265-209=56=8×7+0$, , $209-6=29×7+0$, , $265-6=37×7+0$
Congruence et opérations
Soient $a$ , $b$, $c$ et $d$ des entiers relatifs et $n$ un entier naturel non nul.
Si $a≡b$ $[n]$, et si $c≡d$ $[n]$, alors:
$a+c≡b+d$ $[n]$ $a-c≡b-d$ $[n]$ $ac≡bd$ $[n]$ $a^p≡b^p$ $[n]$ (pour tout naturel $p$)
Conséquences:
Si $a≡b$ $[n]$, alors:
$a+c≡b+c$ $[n]$ $a-c≡b-c$ $[n]$ $ac≡bc$ $[n]$
 Exemple
Exemple
Résoudre l'équation $5x≡2$ $[3]$ en raisonnant par disjonction de cas.
Corrigé
On a: soit $x≡0$ $[3]$, soit $x≡1$ $[3]$, soit $x≡2$ $[3]$.
- $x≡0$ $[3]$ $⇔$ $5x≡5×0$ $[3]$ $⇔$ $5x≡0$ $[3]$. Cela ne convient pas.
-
$x≡1$ $[3]$ $⇔$ $5x≡5×1$ $[3]$ $⇔$ $5x≡5$ $[3]$.
Or: $5≡2$ $[3]$. Donc: $x≡1$ $[3]$ $⇔$ $5x≡2$ $[3]$. Cela convient parfaitement. -
$x≡2$ $[3]$ $⇔$ $5x≡5×2$ $[3]$ $⇔$ $5x≡10$ $[3]$.
Or: $10≡1$ $[3]$. Donc: $x≡2$ $[3]$ $⇔$ $5x≡1$ $[3]$. Cela ne convient pas.
On a donc prouvé que: $5x≡2$ $[3]$ $⇔$ $x≡1$ $[3]$.
Les solutions cherchées sont donc les nombres de la forme $3k+1$ (où $k$ est un entier relatif).
On peut aussi écrire: $S=\{3k+1, k∈ℤ\}$
 Exemple
Exemple
Montrer que, pour tout naturel $n$, $5^{2n}-1$ est un multiple de 8.
Corrigé
On a: $5^2=25=8×3+1$ et $0≤1$ < $8$
Donc: $5^2≡1$ $[8]$.
Et par là: $(5^2)^n≡1^n$ $[8]$. Soit: $5^{2n}≡1$ $[8]$.
Et donc: $5^{2n}-1≡1-1$ $[8]$. Soit: $5^{2n}-1≡0$ $[8]$
Et cela prouve que $5^{2n}-1$ est un multiple de 8.
II PGCD
Définition
Soient $a$ et $b$ deux entiers relatifs non nuls.
Le plus grand commun diviseur à $a$ et $b$ s'appelle PGCD de $a$ et $b$, et il se note $PGCD(a;b)$.
Lemme d'Euclide
Soient $a$ et $b$ deux entiers relatifs non nuls.
Si $a=bq+r$, alors $PGCD(a;b)=PGCD(b;r)$
Savoir faire
Déterminer le PCGD de 2 entiers à l'aide de l'algorithme d'Euclide (comme dans l'exemple ci-dessous).
 Exemple
Exemple
Déterminons $PGCD(468;1365)$ à l'aide de l'algorithme d'Euclide.
Il est clair que $PGCD(468;1365)=PGCD(1365;468)$.
On va effectuer des divisions euclidiennes successives et utiliser le lemme d'Euclide.
Etape 1: $1365=468×2+429$ avec $0≤429 < 468$
Etape 2: $468=429×1+39$ avec $0≤39 < 429$
Etape 3: $429=39×11+0$
On a donc: $PGCD(1365;468)=PGCD(468;429)=PGCD(429;39)=PGCD(39;0)=39$
Donc finalement: $PGCD(468;1365)=39$
Propriété
Soient $a$ et $b$ deux entiers relatifs non nuls.
Les diviseurs communs à $a$ et $b$ sont les diviseurs de $PGCD(a;b)$
 Exemple
Exemple
On a vu dans l'exemple précédent que $PGCD(468;1365)=39$.
Par conséquent, les diviseurs communs à 468 et 1365 sont ceux de 39.
Pour information, il s'agit de 1, 3, 13, 39, -1, -3, -13 et -39.
Définition
Soient $a$ et $b$ deux entiers relatifs non nuls.
$a$ et $b$ sont premiers entre eux si et seulement si $PGCD(a;b)=1$.
Définition
Soient $a$ et $b$ deux entiers relatifs non nuls.
${a}/{b}$ est irréductible si et seulement si $a$ et $b$ sont premiers entre eux.
Identité de Bézout
Soient $a$ et $b$ deux entiers relatifs non nuls.
Si $d=PGCD(a;b)$, alors il existe des entiers relatifs $u$ et $v$ tels que $au+bv=d$.
 Exemple
Exemple
On a vu dans l'exemple précédent que $PGCD(468;1365)=39$.
alors il existe des entiers relatifs $u$ et $v$ tels que $468u+1365v=39$.
On peut trouver $u$ et $v$ en "remontant" l'algorithme d'Euclide, en isolant les restes obtenus, et en procédant par substitutions successives.
Ainsi, l'étape 2 nous donne: $468=429×1+39$, et par là: $468-429×1=39$ (a).
Puis, l'étape 1 nous donne: $1365=468×2+429$, et par là: $1365-468×2=429$ (b).
Et en reportant dans (a), on obtient: $468-(1365-468×2)×1=39$
Soit, en développant: $468-1365+468×2=39$.
Soit: $468×3+1365×(-1)=39$
$u=3$ et $v=-1$ conviennent.
Le couple $(u;v)$ n'est pas unique. Par exemple, $u=-32$ et $v=11$ conviennent également.
Ce nouveau couple a été trouvé en utilisant un tableur.
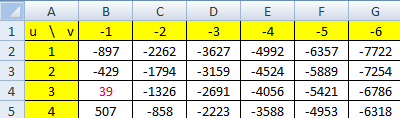
La formule entrée dans la cellule B2 et recopiée vers la droite et vers le bas fut =468*\$A2+1365*B\$1
Elle a donné $39$ pour $u=3$ et $v=-1$, et $-39$ pour $u=32$ et $v=-11$.
On rappelle que les $ permettent de bloquer la lettre ou le nombre qu'ils suivent lors de la recopie.
Théorème de Bézout
Soient $a$ et $b$ deux entiers relatifs non nuls.
$a$ et $b$ sont premiers entre eux si et seulement si il existe des entiers relatifs $u$ et $v$ tels que $au+bv=1$.
 Exemple
Exemple
Soit $a$ un entier relatif et $n$ un entier naturel au moins égal à 2.
On dit que $a$ admet un inverse modulo $n$ si et seulement si il existe un entier relatif $b$ tel que $ab≡1$ $[n]$.
Le relatif $b$ est alors un inverse de $a$ modulo $n$
- Montrer que, si $a$ et $n$ sont premiers entre eux, alors $a$ admet un inverse modulo $n$.
- Montrer que 15 et 22 sont premiers entre eux, et déterminer un inverse de 15 modulo 22.
- Résoudre l'équation (E) $15x≡12$ $[22]$ en utilisant l'inverse de 15 modulo 22.
Corrigé
- $a$ et $n$ sont premiers entre eux, donc, d'après le Théorème de Bézout, il existe des entiers relatifs $u$ et $v$ tels que $au+nv=1$.
Donc: $au=-nv+1$, et il est clair que $0≤1 < n$. Donc le reste de la division euclidienne de $au$ par $n$ vaut 1, ce qui prouve que: $au≡1$ $[n]$.
Il existe donc un entier relatif $u$ tel que $au≡1$ $[n]$. Donc $a$ admet un inverse modulo $n$. -
On va montrer que $PGCD(15;22)=1$ par l'algorithme d'Euclide.
Etape 1: $22=15×1+7$ avec $0≤7 < 15$
Etape 2: $15=7×2+1$ avec $0≤1 < 7$
Etape 3: $7=1×7+0$
On a donc: $PGCD(15;22)=PGCD(22;15)=PGCD(15;7)=PGCD(7;1)=1$
Donc 15 et 22 sont premiers entre eux.
Il existe donc des entiers relatifs $u$ et $v$ tels que $15u+22v=1$.
On peut trouver $u$ et $v$ en "remontant" l'algorithme d'Euclide, en isolant les restes obtenus, et en procédant par substitutions successives.
Ainsi, l'étape 2 nous donne: $15-7×2=1$ (a).
Puis, l'étape 1 nous donne: $22-15×1=7$.
Et en reportant dans (a), on obtient: $15-(22-15×1)×2=1$
Soit, en développant: $15×3+22×(-2)=1$
$u=3$ et $v=-2$ conviennent.
On a donc: $15×3+22×(-2)=1$, et par là: $15×3=22×2+1$.
Et comme $0≤1 < 22$, cela prouve que: $15×3≡1$ $[22]$.
Un inverse de 15 modulo 22 est donc 3. -
Résolvons l'équation (E) $15x≡12$ $[22]$
(E) $⇔$ $15×3x≡12×3$ $[22]$ $⇔$ $45x≡36$ $[22]$
Or, comme $15×3≡1$ $[22]$, on a: $15×3x≡1×x$ $[22]$, soit: $45x≡x$ $[22]$
Et par là, on obtient: (E) $⇔$ $x≡36$ $[22]$
Soit: (E) $⇔$ $x≡14$ $[22]$
Les solutions cherchées sont donc les nombres de la forme $22k+14$ (où $k$ est un entier relatif).
On peut aussi écrire: $S=\{22k+14, k∈ℤ\}$
Théorème de Gauss
Soient $a$, $b$ et $c$ trois entiers relatifs non nuls.
Si $a$ divise le produit $bc$, et si $a$ et $b$ sont premiers entre eux, alors $a$ divise $c$.
 Exemple
Exemple
Résoudre l'équation $15x=22y$ dans $ℤ$.
Corrigé
On a $15x=22y$, et par là: 15 divise le produit $22y$.
Or, on a vu dans l'exemple précédent que 15 et 22 sont premiers entre eux.
Donc, d'après le théorème de Gauss, 15 divise $y$.
Donc il existe un relatif $k$ tel que $y=15k$.
Et par là, en reportant dans $15x=22y$, on obtient: $15x=22×15k$, soit: $x=22k$
Et réciproquement, on vérifie que, pour tout relatif $k$, le couple $(22k;15k)$ convient.
En effet, on a: $15×22k=22×15k$ .
Finalement, les solutions de l'équation $15x=22y$ dans $ℤ$ sont les couples $(22k;15k)$ avec $k$ entier relatif.
Définition et propriété
Soient $a$, $b$ et $c$ trois entiers relatifs non nuls.
Une équation dans $ℤ$ du type $ax+by=c$ s'appelle une équation diophantienne.
Une telle équation admet des solutions si et seulement si $c$ est un multiple de $PGCD(a;b)$.
Savoir faire
Savoir résoudre une équation diophantienne (comme dans l'exemple ci-dessous).
 Exemple
Exemple
On considère l'équation diophantienne (E) $2x+5y=4$.
- Trouver 2 entiers $u$ et $v$ tels que $2u+5v=1$
- En déduire une solution particulière $(x_0;y_0)$ de l'équation diophantienne $2x+5y=4$.
- Montrer que: (E) $⇔$ $2(x-x_0)=5(y_0-y)$
En déduire les solutions de (E).
Corrigé
- On a: $2×(-2)+5×1=1$ Donc $(u;v)=(-2;1)$ convient.
On note ici le PGCD de 2 et 5 vaut 1, et que 4 en est un multiple. L'équation (E) admet donc des solutions. - Comme $2×(-2)+5×1=1$, on obtient: $2×(-2)×4+5×1×4=1×4$, soit: $2×(-8)+5×4=4$.
Donc $(x_0;y_0)=(-8;4)$ est une solution particulière de (E). - On a donc: $2x_0+5y_0=4$.
Donc: (E) $⇔$ $2x+5y=2x_0+5y_0$ $⇔$ $2(x-x_0)=5(y_0-y)$
On a: $2(x-x_0)=5(y_0-y)$, et par là: 2 divise le produit $5(y_0-y)$.
Or, on a vu que 2 et 5 sont premiers entre eux.
Donc, d'après le théorème de Gauss, 2 divise $y_0-y$.
Donc il existe un relatif $k$ tel que $y_0-y=2k$.
Et par là, en reportant dans $2(x-x_0)=5(y_0-y)$, on obtient: $2(x-x_0)=5×2k$, soit: $x-x_0=5k$
Finalement, on a: $x=x_0+5k=-8+5k$ et $y=y_0-2k=4-2k$
Et réciproquement, on vérifie que, pour tout relatif $k$, le couple $(-8+5k;4-2k)$ convient.
En effet, on a: $2(-8+5k)+5(4-2k)=4$ .
En conclusion, les solutions de l'équation (E) dans $ℤ$ sont les couples $(-8+5k;4-2k)$ avec $k$ entier relatif.
Corollaire du théorème de Gauss
Soient $a$, $b$ et $c$ trois entiers relatifs non nuls.
Si $b$ et $c$ divisent $a$, et si $b$ et $c$ sont premiers entre eux, alors le produit $bc$ divise $a$.
 Exemple
Exemple
On pose $x=n(n+2)(n^2+2n+1)$, où $n$ est un entier relatif.
Montrer que $x$ est divisible par 3.
Montrer que $x$ est divisible par 12.
Corrigé
On a $x=n(n+2)(n^2+2n+1)=n(n+2)(n+1)^2=n(n+1)(n+2)×(n+1)$.
Or $n$, $n+1$ et $n+2$ sont 3 entiers consécutifs.
Donc l'un des 3 est divisible par 3.
Et par là, $x$ est divisible par 3.
Montrons que $x$ est divisible par 4.
On a $x=n(n+1)×(n+1)(n+2)$.
Or $n$ et $n+1$ sont 2 entiers consécutifs.
Donc l'un des 2 est divisible par 2.
Et par là, $n(n+1)$ est divisible par 2.
Et de même, $(n+1)(n+2)$ est divisible par 2.
Par conséquent, $x$ est divisible par $2×2=4$.
Finalement, 3 et 4 divisent $x$.
Or, comme $3×(-1)+4×1=1$, les entiers $3$ et $4$ sont premiers entre eux.
Donc, d'après le corollaire du théorème de Gauss , $x$ est divisible par $3×4=12$.
III Les nombres premiers
Définitions
Un entier naturel est premier s'il a exactement 2 diviseurs naturels, 1 et lui-même.
 Exemple
Exemple
Le nombre 0 n'est pas premier car il possède plus de 2 diviseurs naturels (en l'occurence une infinité).
Le nombre 1 n'est pas premier car il ne possède qu'un seul diviseur naturel (en l'occurence 1).
Le nombre 2 est premier car il a exactement 2 diviseurs naturels, 1 et lui-même.
Le nombre 3 est premier car il a exactement 2 diviseurs naturels, 1 et lui-même.
Les naturels pairs supérieurs à 3 ne sont pas premiers car ils possèdent au moins un autre diviseur naturel que 1 et eux-mêmes. (en l'occurence 2).
Le nombre 5 est premier car il a exactement 2 diviseurs naturels, 1 et lui-même.
Propriété
Soit $n$ un entier naturel au moins égal à 4.
Si $n$ n'est pas premier, alors il possède au moins un diviseur premier $p$ tel que $2≤p ≤ √{n}$
Test de primalité
Si $n$ n'est divisible par aucun nombre premier inférieur ou égal à $√{n}$, alors $n$ est premier.
 Exemple
Exemple
Montrons que 37 est premier.
On a: $√{37}≈6,08$.
Or les nombres premiers inférieur ou égal à $√{37}$ sont: 2, 3 et 5.
Et 37 n'est divisible par aucun d'eux.
Donc 37 est premier.
Propriété
Les vingt-cinq nombres premiers inférieurs à 100 sont :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, et 97.
Propriété
Il existe une infinité de nombres premiers, et par là, il n'existe pas de plus grand nombre premier.
Décomposition en produit de facteurs premiers
Si $n$ est un entier naturel au moins égal à 2, alors il se décompose en produit de facteurs premiers de la façon suivante:
$n=p_1^{α_1}×p_2^{α_2}×p_3^{α_3}×...×p_k^{α_k}$
où $p_1$, $p_2$, $p_3$, ... ,$p_k$ sont des nombres premiers distincts rangés dans l'ordre croissant
et où $α__1$, $α__2$, $α__3$, ... ,$α__k$ sont des entiers naturels non nuls.
Cette décomposition est unique.
Les diviseurs naturels de $n$ sont de la forme $p_1^{β_1}×p_2^{β_2}×p_3^{β_3}×...×p_k^{β_k}$
où $0≤β_i ≤ α_i$ pour tout $i$ entre 0 et $k$.
 Exemple
Exemple
Déterminer la liste des diviseurs naturels de 234.
Corrigé
On cherche la décomposition de 234 en produit de facteurs premiers.
On obtient: $234=2×117=2×3×39=2×3×3×13$
Soit: $234=2×3^2×13$
Par conséquent, les diviseurs de 234 sont de la forme $2^a×3^b×13^c$
où $0≤a ≤ 1$, $0≤b ≤ 2$ et $0≤c ≤ 1$ .
On peut alors dresser l'arbre de dénombrement suivant.
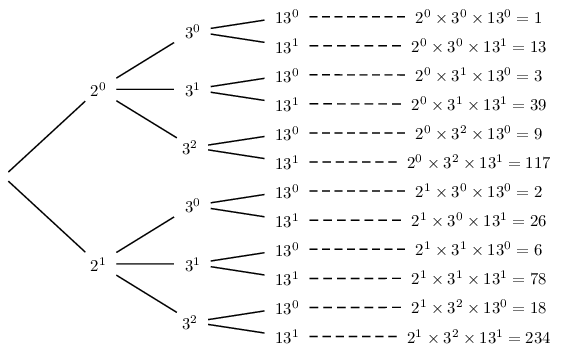
L'ensemble des diviseurs de 234 est donc:
$S=\{1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117, 234\}$
Propriété
Si $a$ et $b$ deux entiers naturels au moins égaux à 2, alors $PGCD(a;b)$ s'obtient en effectuant le produit des facteurs premiers communs aux décompositions de $a$ et de $b$, chaque facteur étant affecté du plus petit exposant de chacune des 2 décompositions.
 Exemple
Exemple
Cherchons $PGCD(468;1365)$ à l'aide de la propriété ci-dessus.
On obtient aisément: $468=2^2×3^2×13$ et $1365=3×5×7×13$
Donc: $PGCD(468;1365)=3^1×13^1=3×13=39$
C'est autrement plus rapide que l'algorithme d'Euclide si les décompositions sont faciles à trouver...
Petit théorème de Fermat
Soit $n$ un entier naturel.
Si $p$ est un nombre premier qui ne divise pas $n$, alors $n^{p-1}≡ 1 [p]$
Cela équivaut à: "$n^{p-1}- 1$ est divisible par $p$"
Corollaire du petit théorème de Fermat
Soit $n$ un entier naturel.
Si $p$ est un nombre premier, alors $n^{p}≡ n [p]$
 Exemple
Exemple
Montrer, à l'aide du petit théorème de Fermat, que, pour tout naturel $n$, $n^{11}-n$ est divisible par 33.
Corrigé
On décompose: $33=3×11$.
Comme 11 est premier, $n^{11}≡ n [11]$ (d'après le corollaire du petit théorème de Fermat).
Donc $n^{11}-n$ est divisible par 11.
Par ailleurs, on a: soit $n≡0 [3]$, soit $n≡1 [3]$ ,soit $n≡2 [3]$.
-
Si $n≡0 [3]$, alors: $n^{11}≡ 0^{11} [3]$, c'est à dire: $n^{11}≡ 0 [3]$.
Et, par différence, on a: $n^{11}-n≡ 0-0 [3]$, , c'est à dire que $n^{11}-n$ est divisible par 3. -
Si $n≡1 [3]$, alors: $n^{11}≡ 1^{11} [3]$, c'est à dire: $n^{11}≡ 1 [3]$.
Et, par différence, on a: $n^{11}-n≡ 0 [3]$, , c'est à dire que $n^{11}-n$ est divisible par 3. -
Si $n≡2 [3]$, alors: $n^{11}≡ 2^{11} [3]$, c'est à dire: $n^{11}≡ 2048 [3]$.
Et comme $2048=682×2+2$, on obtient: $n^{11}≡ 2 [3]$.
Et, par différence, on a: $n^{11}-n≡ 0 [3]$, , c'est à dire que $n^{11}-n$ est divisible par 3.
Dans tous les cas, $n^{11}-n$ est divisible par 3.
Finalement, $n^{11}-n$ est divisible par 3 et par 11, nombres premiers entre eux.
Donc, d'après un corollaire du théorème de Gauss, $n^{11}-n$ est divisible par leur produit, c'est à dire par 33.