Orthogonalité
Exercice 3
Le plan est rapporté à un repère orthonormé (O,I,J).
1. Faire une figure en plaçant le point $F(0;0,25)$ et la droite $d$ d'équation $y=-0,25$.
2. Soit $M$ un point du plan. Soit $H$ le projeté orthogonal de $M$ sur la droite $d$.
On suppose que $FM=MH$.
Placer sur un même dessin le (ou les) point(s) $M$ convenable(s) dans chacun des cas suivants:
$FM=3$ $FM=2$ $FM=1$ $FM=0,25$
3. Soit $(x;y)$ les coordonnées d'un point $M$ dont le projeté orthogonal sur la droite $d$ s'appelle $H$.
Il est clair que $H(x;-0,25)$.
Montrer que $FM=MH$ si et seulement si $y=x^2$.
4. Quel est l'ensemble des points M ?
Corrigé
1. 2. Voici la construction des deux points M tels que $FM=MH=3$.
On rappelle que, si $H$ est le projeté orthogonal de $M$ sur la droite $d$, alors la distance entre M et la droite $d$ est MH.
Et donc, si, par exemple, MH=3, alors M se situe à une distance de 3 de la droite $d$.
M est donc sur l'une des 2 droites (parallèles à $d$) situées à une distance de 3 de la droite $d$ du dessin.
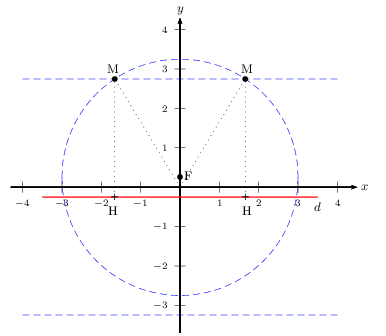
Par ailleurs, comme FM=3, M est sur le cercle de centre F de rayon 3. On a tracé ce cercle sur le dessin.
Or, une seule des deux droites situées à une distance de 3 de la droite $d$ coupe le cercle précédent.
Tout point M convenable se trouve donc sur cette droite et sur le cercle.
Les deux points situés à l'intersection de la droite et du cercle conviennent.
On procède de même pour tous les autres points M.
On obtient à chaque fois deux points M, sauf pour $FM=0,25$ qui donne un seul point (l'origine).
D'où la figure suivante.
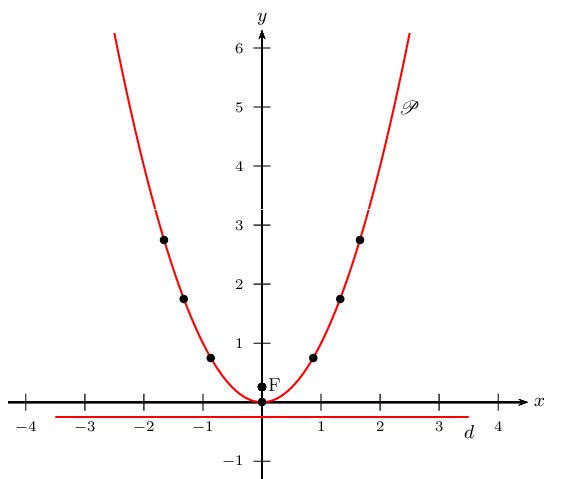
Tous les points se trouvent sur la courbe P qui semble être une parabole.
3. Soit $(x;y)$ les coordonnées d'un point $M$ dont le projeté orthogonal sur la droite $d$ s'appelle $H$.
On a: $FM=MH$ $ ⇔$ $FM^2=MH^2$ (car les distances FM et MH sont nécessairement positives)
Soit: $FM=MH$ $ ⇔$ $(x-0)^2+(y-0,25)^2=(x-x)^2+(-0,25-y)^2$
Soit: $FM=MH$ $ ⇔$ $x^2+y^2-2×y×0,25+0,25^2=0^2+(-0,25)^2-2×(-0,25)×y+y^2$
Soit: $FM=MH$ $ ⇔$ $x^2+y^2-0,5y+0,0625=0+0,0625+0,5y+y^2$
Soit: $FM=MH$ $ ⇔$ $x^2=0,5y+0,5y$
Soit: $FM=MH$ $ ⇔$ $x^2=y$ c.q.f.d.
4. Par conséquent, l'ensemble des points M est la parabole $\P$ de sommet O d'équation $y=x^2$.