 Généralités sur les fonctions
Généralités sur les fonctions
Exercice 6
On considère la fonction $f$ définie par $f(x)=x^2-2√{x}+2$ sur l'intervalle $[0;4]$.
Cette fonction admet le tableau de variation suivant:
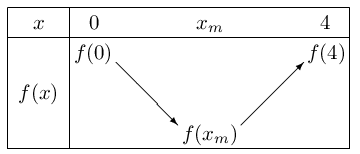
Le programme suivant est écrit en langage Python.
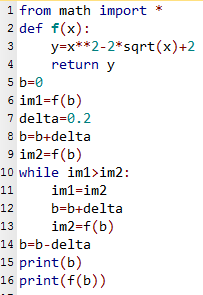
- Donner les valeurs successives prises par les variables b, im1 et im2 lors de l'exécution du programme.
- Quel est l'utilité d'un tel programme ?
- A l'aide d'un ordinateur, faites fonctionner ce programme avec delta=0.01 (à la ligne 7). Quelles sont les valeurs affichées ?
Solution...
Corrigé
-
b=0 im1=f(0)=2 b=0+0,2=0,2 im2=f(0,2)$≈$1,45
Comme im1>im2, on commence une première boucle
im1$≈$1,45 b=0,2+0,2=0,4 im2=f(0,4)$≈$0,90
Comme im1>im2, on commence une seconde boucle
im1$≈$0,90 b=0,4+0,2=0,6 im2=f(0,6)$≈$0,81
Comme im1>im2, on commence une troisième boucle
im1$≈$0,81 b=0,6+0,2=0,8 im2=f(0,8)$≈$0,85
Cette fois-ci, im1$≤$im2; les boucles s'arrêtent.
b=0,8-0,2=0,6
Il s'affiche la valeur de b, c'est à dire 0,6
Il s'affiche l'image de b, c'est à dire environ 0,81.
Si vous faites fonctionner ce programme sur votre ordinateur, vous noterez que la valeur affichée n'est pas 0,6 mais 0,6000000000000001.
Cela est dû au fait que vote ordinateur ne manipule que des nombres sous forme binaire (écrits avec des 0 et des 1). Or, l'écriture en binaire de certains nombres décimaux utilise une infinité de 0 et de 1; ces nombres décimaux sont donc remplacés par leurs valeurs approchées pour être stockés dans la machine, ce qui explique alors des résultats souvent approximatifs. - Un tel programme balaie les valeurs de $x$ à partir de 0 avec un pas de 0,2, et ce balayage continue tant que les images de ces $x$ diminuent.
Or, d'après le tableau de variation donné, $f$ admet un minimum $f(x_m)$ atteint en $x_m$.
Le but est donc de déterminer une approximation de $x_m$ et du minimum $f(x_m)$ par balayage. Ici, on obtient: f(0,4)>f(0,6) mais f(0,6)$≤$f(0,8).
Donc on peut avoir:
soit $x_m$=0,6,
soit 0,4<$x_m$<0,6 si f(0,4)>f($x_m$) et f($x_m$)<f(0,6),
soit 0,6<$x_m≤$0,8 si f(0,6)>f($x_m$) et f($x_m$) $≤$f(0,8)
Donc $x_m$ est compris entre 0,4 et 0,8.
0,6 est une valeur approchée de $x_m$ à 0,2 près. - Si l'on fait fonctionner le programme à l'aide d'un ordinateur avec delta=0.01 (ligne 7), les valeurs affichées nous donnent:
$x_m≈0,63$ et $f(x_m)≈0,809$
0,63 est une valeur approchée de $x_m$ à 0,01 près.