Corrigé

Le plan est rapporté à un repère orthonormé (O,I,J).
On considère les points $A(1;2)$, $B(4;0)$, $C(6;1)$ et $D(x_D;y_D)$.
1. $M(x;y)∈(BC)$ $⇔$ ${BM}↖{→}$ et ${BC}↖{→}$ sont colinéaires.
Or ${BM}↖{→}$ a pour coordonnées: $(x-4;y-0)=(x-4;y)$.
Et ${BC}↖{→}$ a pour coordonnées: $(6-4;1-0)=(2;1)$.
Donc: $M(x;y)∈(BC)$ $⇔$ $(x-4)×1-2×y=0$
Donc: $M(x;y)∈(BC)$ $⇔$ $x-4-2y=0$
Ceci est une équation cartésienne de la droite (BC).
On continue: $M(x;y)∈(BC)$ $⇔$ $-2y=-x+4$ $⇔$ $y={-1}/{-2}x+{4}/{-2}$
Donc: $M(x;y)∈(BC)$ $⇔$ $y=0,5x-2$.
Ceci est l'équation réduite de la droite (BC)
A retenir: la méthode utilisant la colinéarité de vecteurs pour obtenir facilement une équation de droite.

2. La droite $d_1$ est parallèle à la droite (BC).
Or (BC) a pour coefficient directeur $0,5$.
Donc $d_1$ a aussi pour coefficient directeur $0,5$.
Et donc $d_1$ admet une équation du type: $y=0,5x+b$.
Or $d_1$ passe par $A(1;2)$. Donc: $2=0,5×1+b$.
Donc: $2-0,5=b$. Soit: $1,5=b$.
Donc $d_1$ admet pour équation réduite: $y=0,5x+1,5$.

3. La droite (AB) admet pour coefficient directeur: ${y_B-y_A}/{x_B-x_A}={0-2}/{4-1}=-{2}/{3}$.
Or, $d_2$, d'équation : $y=-{2}/{3}x+5$, a aussi pour coefficient directeur $-{2}/{3}$.
Donc $d_2$ et (AB) sont parallèles.
Il reste à prouver que $d_2$ passe par C.
On calcule: $-{2}/{3}x_C+5=-{2}/{3}×6+5=-4+5= 1=y_C$.
Donc les coordonnées de C vérifient l'équation de $d_2$.
Donc $d_2$ passe bien par C.    c.q.f.d.

4. Les coordonnées du point $D(x_D;y_D)$, intersection des droites $d_1$ et $d_2$, vérifient à la fois les équations de $d_1$ et de $d_2$.
Ces coordonnées sont donc solution du système:
$\{\table y={1}/{2}x+{3}/{2}; y=-{2}/{3}x+5$
En substituant au $y$ de la seconde ligne la formule donnée par la première ligne, on obtient:
${1}/{2}x+{3}/{2}=-{2}/{3}x+5$ $⇔$ ${1}/{2}x+{2}/{3}x+=5-{3}/{2}$ $⇔$ $({1}/{2}+{2}/{3})x={10}/{2}-{3}/{2}$
$⇔$ $({3}/{6}+{4}/{6})x={7}/{2}$ $⇔$ ${7}/{6}x={7}/{2}$ $⇔$ $ x={7}/{2}×{6}/{7}=3$
Et, en reportant dans la première ligne, on obtient: $y={1}/{2}×3+{3}/{2}=3$
Donc, finalement, le point $D$ a pour coordonnées $(3;3)$.

5. Une figure est bien utile pour conjecturer!

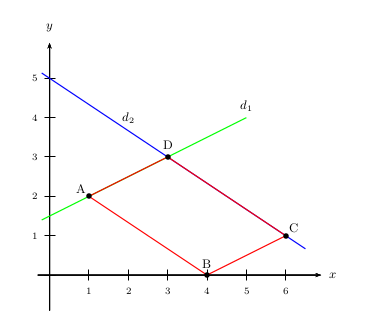
Nous conjecturons que le quadrilatère ABCD est un parallélogramme.
Démontrons le!
On a vu que $d_1$ est parallèle à (BC). Or $d_1$ passe par A et D. Donc (AD) est parallèle à (BC).
Par ailleurs, on a vu que $d_2$ est parallèle à (AB). Or $d_2$ passe par C et D. Donc (CD) est parallèle à (AB).
Donc, finalement, le quadrilatère non aplati ABCD a ses côtés deux à deux parallèles.
Par conséquent, ABCD est un parallélogramme.
Remarque: le caractère "non aplati" du quadrilatère est indispensable, sinon, n'importe quel quadrilatère aplati serait un parallélogramme!
Pour se dispenser de cette hypothèse, il suffit, par exemple, de démontrer que les vecteurs ${AB}↖{→}$ et ${DC}↖{→}$ sont égaux, ce qui justifie de façon rigoureuse que ABCD est effectivement un paralléogramme.